Danh Mục Sách
- Thiếu nhi
- Giáo khoa - Tham khảo
- Văn học
- Tâm lý - Kỹ năng sống
- Manga - Comic
- Sách học ngoại ngữ
- Kinh Tế
- Khoa học kỹ thuật
- Lịch Sử - Địa Lý - Tôn Giáo
- Nuôi Dạy Con
- Chính Trị - Pháp Lý - Triết Học
- Tiểu Sử Hồi Ký
- Đam Mỹ
- Nữ Công Gia Chánh
- Văn Hóa - Nghệ Thuật - Du Lịch
- Phong Thủy - Kinh Dịch
- Từ điển
- Âm Nhạc - Mỹ Thuật - Thời Trang
- Thể Dục Thể thao - Giải Trí
- Báo - Tạp Chí
- Giáo trình
- Làm Vườn - Thú Nuôi
- Mystery Box
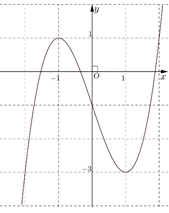
 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
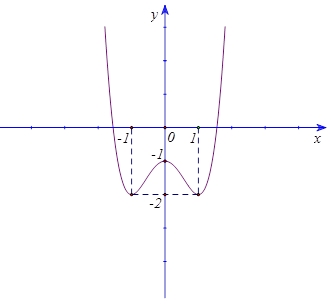
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?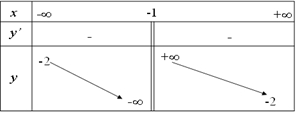
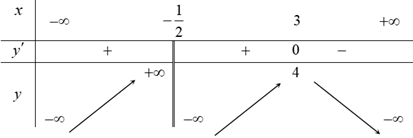
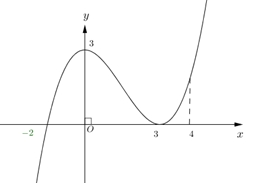
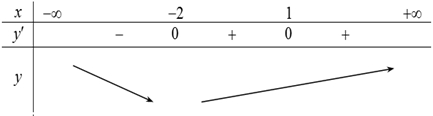 Vậy hàm số đồng biến trên khoảng \(\left( { – 2; + \infty } \right)\).
Vậy hàm số đồng biến trên khoảng \(\left( { – 2; + \infty } \right)\).