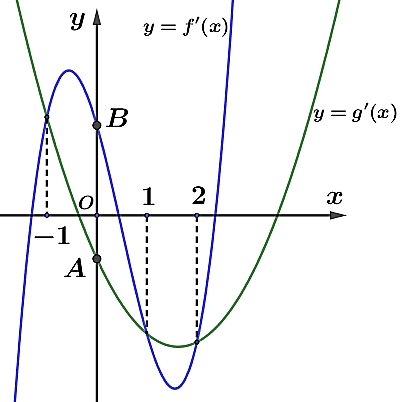
Ta có:\(g'\left( x \right) = \frac{{f'\left( x \right)\left( {2f\left( x \right) – 4} \right)\left( {{f^2}\left( x \right) – 4f\left( x \right) – m} \right)}}{{\left| {{f^2}\left( x \right) – 4f\left( x \right) – m} \right|}}.f'\left( {\left| {{f^2}\left( x \right) – 4f\left( x \right) – m} \right|} \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {f'\left( x \right) = 0\,\,\left( 1 \right)} \\ {2f\left( x \right) – 4 = 0 \Leftrightarrow f\left( x \right) = 2\,\,\,\left( 2 \right)} \\ {{f^2}\left( x \right) – 4f\left( x \right) – m = 0 \Leftrightarrow {f^2}\left( x \right) – 4f\left( x \right) = m\,\,\,\left( 3 \right)} \\ {\left| {{f^2}\left( x \right) – 4f\left( x \right) – m} \right| = – 1\,\,\left( {vo\,ly} \right)} \\ {\left| {{f^2}\left( x \right) – 4f\left( x \right) – m} \right| = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{f^2}\left( x \right) – 4f\left( x \right) – m = 2} \\ {{f^2}\left( x \right) – 4f\left( x \right) – m = – 2} \end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{f^2}\left( x \right) – 4f\left( x \right) = m + 2\,\,\left( 4 \right)} \\ {{f^2}\left( x \right) – 4f\left( x \right) = m – 2\,\,\left( 5 \right)} \end{array}} \right.} \right.} \end{array}} \right.\)
Dễ thấy \(\left( 1 \right)\) có 2 nghiệm đơn (vì có 2 cực trị) và \(\left( 2 \right)\) có 3 nghiệm đơn Vậy tổng số nghiệm đơn của phương trình \(\left( 3 \right);\,\left( 4 \right);\,\left( 5 \right)\) là 12 thì thỏa mãn
Đặt \(u = u\left( x \right) = {f^2}\left( x \right) – 4f\left( x \right) \Rightarrow u' = 2f'\left( x \right)\left( {f\left( x \right) – 2} \right) \Rightarrow u' = 0 \Leftrightarrow \left[ \begin{gathered} x \in \left\{ { – 1;2} \right\} \hfill \\ x \in \left\{ {a;b;c} \right\} \hfill \\ \end{gathered} \right.\).
Các nghiệm trên được sắp thứ tự từ nhỏ đến lớn như sau: \(a < - 1 < b < 2 < c\).
Bảng biến thiên của hàm số \(u = {f^2}\left( x \right) – 4f\left( x \right)\).
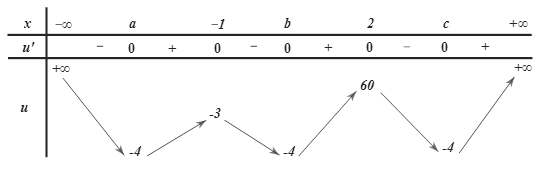
Vậy số giao điểm của các đường thẳng \(y = m – 2;y = m;y = m + 2\) với đồ thị \(u\left( x \right)\) là 12 điểm phân biệt\( \Leftrightarrow \left\{ \begin{gathered} – 3 \leqslant m – 2 < 60 \hfill \\ - 3 \leqslant m + 2 < 60 \hfill \\ \end{gathered} \right. \Leftrightarrow - 1 \leqslant m < 58 \Rightarrow m \in \left\{ { - 1;0;1;...;57} \right\} \Rightarrow S = 1652\).
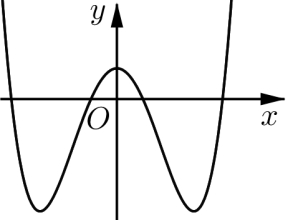
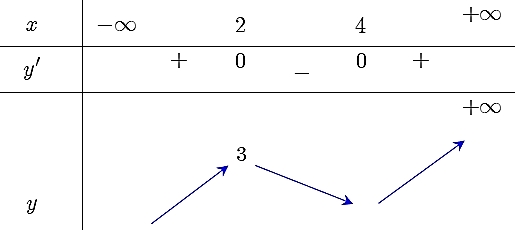 Hàm số nghịch biến trên khoảng nào sau đây?
Hàm số nghịch biến trên khoảng nào sau đây?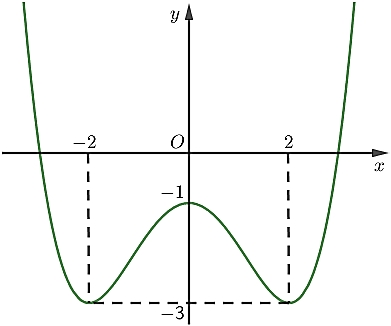
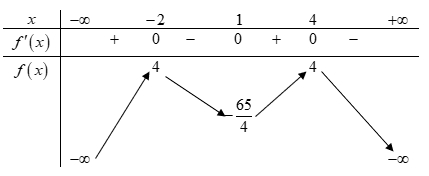 Số nghiệm thực phân biệt của phương trình là
Số nghiệm thực phân biệt của phương trình là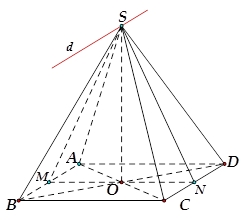 Gọi \(O = AC \cap BD\) và \(M,N\) lần lượt là trung điểm \(AB,CD\). Do \(AC = 6a \Rightarrow AB = \frac{{AC}}{{\sqrt 2 }} = 3a\sqrt 2 \). Đồng thời \(\left( {SAB} \right) \cap \left( {SCD} \right) = d\parallel \,AB\parallel CD\)Dễ dàng chứng minh \(SM \bot AB\) và \(SN \bot CD\) (do \(\Delta SAB,\Delta SCD\)cân tại \(S\)).Suy ra \(\widehat {\left[ {\left( {SAB} \right),\left( {SCD} \right)} \right]} = \widehat {\left( {SM;SN} \right)} = {60^0}\). Từ đó suy ra \(\Delta SMN\) đều hay \(SO = \frac{{MN\sqrt 3 }}{2} = \frac{{AB\sqrt 3 }}{2} = \frac{{3a\sqrt 6 }}{2}\).Vậy \({V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.\frac{{3a\sqrt 6 }}{2}.{\left( {3a\sqrt 2 } \right)^2} = 9\sqrt 6 {a^3}\).
Gọi \(O = AC \cap BD\) và \(M,N\) lần lượt là trung điểm \(AB,CD\). Do \(AC = 6a \Rightarrow AB = \frac{{AC}}{{\sqrt 2 }} = 3a\sqrt 2 \). Đồng thời \(\left( {SAB} \right) \cap \left( {SCD} \right) = d\parallel \,AB\parallel CD\)Dễ dàng chứng minh \(SM \bot AB\) và \(SN \bot CD\) (do \(\Delta SAB,\Delta SCD\)cân tại \(S\)).Suy ra \(\widehat {\left[ {\left( {SAB} \right),\left( {SCD} \right)} \right]} = \widehat {\left( {SM;SN} \right)} = {60^0}\). Từ đó suy ra \(\Delta SMN\) đều hay \(SO = \frac{{MN\sqrt 3 }}{2} = \frac{{AB\sqrt 3 }}{2} = \frac{{3a\sqrt 6 }}{2}\).Vậy \({V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.\frac{{3a\sqrt 6 }}{2}.{\left( {3a\sqrt 2 } \right)^2} = 9\sqrt 6 {a^3}\).
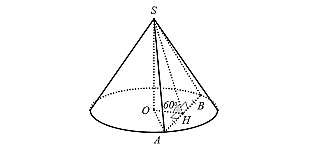 Xét hình nón đỉnh \(S\) có chiều cao \(h = SO = 3a\). Thiết diện của hình nón cắt bởi mặt phẳng \(\left( P \right)\)là tam giác \(SAB\) vuông cân tại \(S\).Kẻ \(OH \bot AB\) và \(SO \bot AB\) nên \(AB \bot \left( {SHO} \right) \Rightarrow AB \bot SH\)Vậy góc giữa mặt phẳng \(\left( P \right)\)và mặt phẳng đáy bằng \(\widehat {SHO} = {60^0}\).Xét \(\Delta OHS\)vuông tại \(O\)có \(OH = SO.\cot \widehat {SHO} = 3a.\cot {60^0} = a\sqrt 3 \); \(SH = \sqrt {O{H^2} + S{O^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {3a} \right)}^2}} = 2a\sqrt 3 \)Tam giác \(SAB\) vuông cân tại \(S\)nên suy ra \(HA = HB = HS = 2a\sqrt 3 \).Xét tam giác \(HAO\) vuông tại \(H\), ta có:\(R = OA = \sqrt {O{H^2} + H{A^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {2a\sqrt 3 } \right)}^2}} = a\sqrt {15} \)Thể tích của khối nón được giới hạn bởi hình nón là: \(V = \frac{1}{3}h.\pi {R^2} = \frac{1}{3}.3a.\pi .{\left( {a\sqrt {15} } \right)^2} = 15\pi {a^3}.\)
Xét hình nón đỉnh \(S\) có chiều cao \(h = SO = 3a\). Thiết diện của hình nón cắt bởi mặt phẳng \(\left( P \right)\)là tam giác \(SAB\) vuông cân tại \(S\).Kẻ \(OH \bot AB\) và \(SO \bot AB\) nên \(AB \bot \left( {SHO} \right) \Rightarrow AB \bot SH\)Vậy góc giữa mặt phẳng \(\left( P \right)\)và mặt phẳng đáy bằng \(\widehat {SHO} = {60^0}\).Xét \(\Delta OHS\)vuông tại \(O\)có \(OH = SO.\cot \widehat {SHO} = 3a.\cot {60^0} = a\sqrt 3 \); \(SH = \sqrt {O{H^2} + S{O^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {3a} \right)}^2}} = 2a\sqrt 3 \)Tam giác \(SAB\) vuông cân tại \(S\)nên suy ra \(HA = HB = HS = 2a\sqrt 3 \).Xét tam giác \(HAO\) vuông tại \(H\), ta có:\(R = OA = \sqrt {O{H^2} + H{A^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {2a\sqrt 3 } \right)}^2}} = a\sqrt {15} \)Thể tích của khối nón được giới hạn bởi hình nón là: \(V = \frac{1}{3}h.\pi {R^2} = \frac{1}{3}.3a.\pi .{\left( {a\sqrt {15} } \right)^2} = 15\pi {a^3}.\) Tổng tất cả các giá trị nguyên của tham số \(m\)để hàm số \(g\left( x \right) = f\left( {\left| {{f^2}\left( x \right) – 4f\left( x \right) – m} \right|} \right)\) có \(17\) điểm cực trị là
Tổng tất cả các giá trị nguyên của tham số \(m\)để hàm số \(g\left( x \right) = f\left( {\left| {{f^2}\left( x \right) – 4f\left( x \right) – m} \right|} \right)\) có \(17\) điểm cực trị là Vậy số giao điểm của các đường thẳng \(y = m – 2;y = m;y = m + 2\) với đồ thị \(u\left( x \right)\) là 12 điểm phân biệt\( \Leftrightarrow \left\{ \begin{gathered} – 3 \leqslant m – 2 < 60 \hfill \\ - 3 \leqslant m + 2 < 60 \hfill \\ \end{gathered} \right. \Leftrightarrow - 1 \leqslant m < 58 \Rightarrow m \in \left\{ { - 1;0;1;...;57} \right\} \Rightarrow S = 1652\).
Vậy số giao điểm của các đường thẳng \(y = m – 2;y = m;y = m + 2\) với đồ thị \(u\left( x \right)\) là 12 điểm phân biệt\( \Leftrightarrow \left\{ \begin{gathered} – 3 \leqslant m – 2 < 60 \hfill \\ - 3 \leqslant m + 2 < 60 \hfill \\ \end{gathered} \right. \Leftrightarrow - 1 \leqslant m < 58 \Rightarrow m \in \left\{ { - 1;0;1;...;57} \right\} \Rightarrow S = 1652\).